Conocer la estructura de las calles es de gran importancia para muchas áreas de conocimento, y últimamente, en la distribución de mercancias, para encontrar zonas mejor posicionadas para instalar puntos de ventas y/o distribución.
Para conocer la estructura de las calles de la ciudad de Ensenada se consideraron las calles como una red y se aplicaron diferentes algoritmos de centralidad para descubrir las diferentes formas en la estructura.
Calles de la ciudad de Ensenada
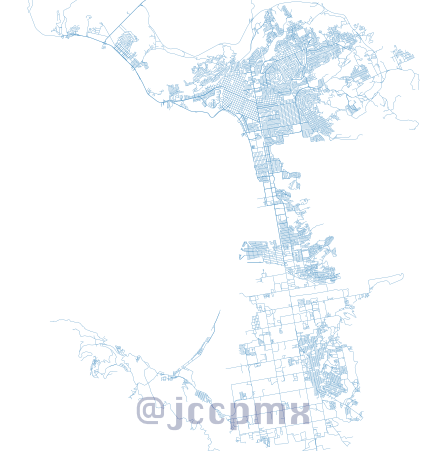
Centralidad cercana
La centralidad de cercanía podría simplificarse como la distancia promedio a todos los demás nodos desde cada nodo.
Se puede medir en toda la red (Centralidad cercana global) o solo dentro de un cierto radio (Centralidad cercana local).
Centralidad cercana local
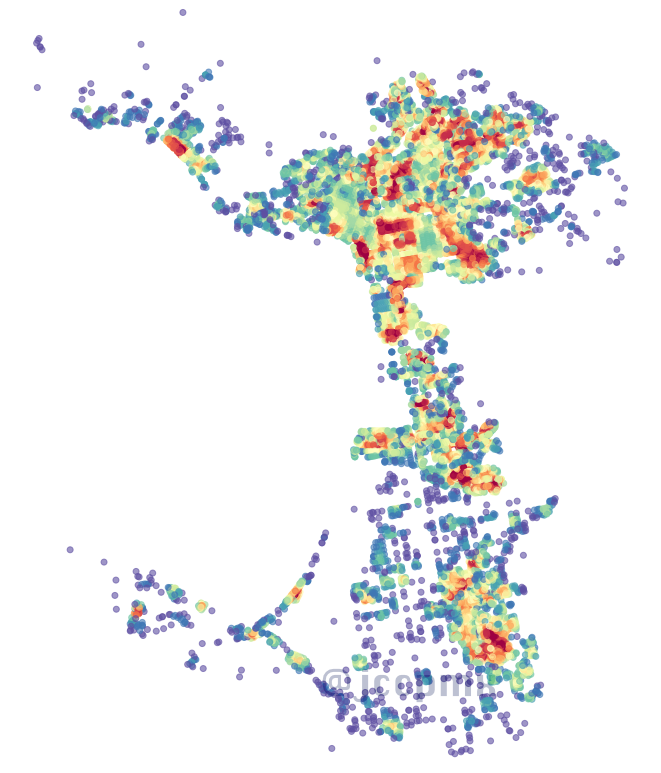
Centralidad cercana global

Centralidad de intermediación
La centralidad de intermediación mide la importancia de cada nodo o borde para viajar a lo largo de la red. Mide cuántas veces se usa cada nodo/arista si caminamos usando los caminos más cortos de un nodo a otro.
Hay dos opciones para medir la intermediación en gráficos: en nodos o en bordes.
Intermediación con nodos
Cuántas veces recorremos el nodo.
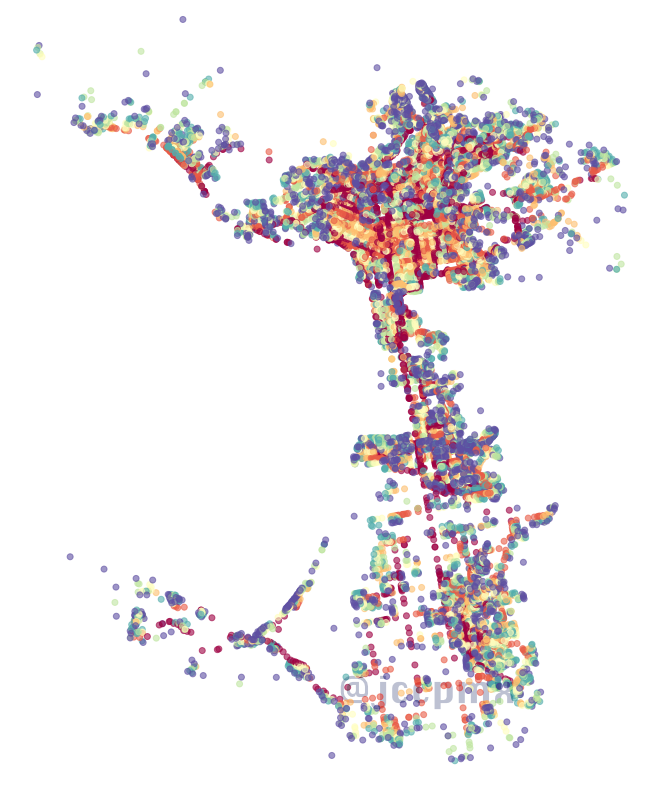
La intermediación con calles
Cuántas veces pasamos por cada calle.

Centralidad straightness
Si bien tanto la cercanía como la intermediación se utilizan generalmente en muchas aplicaciones de análisis de redes, la centralidad de straightness es específica de las redes de calles, ya que requiere un elemento geográfico. Se mide como una relación entre la distancia real y euclidiana mientras se camina de un nodo a otro.
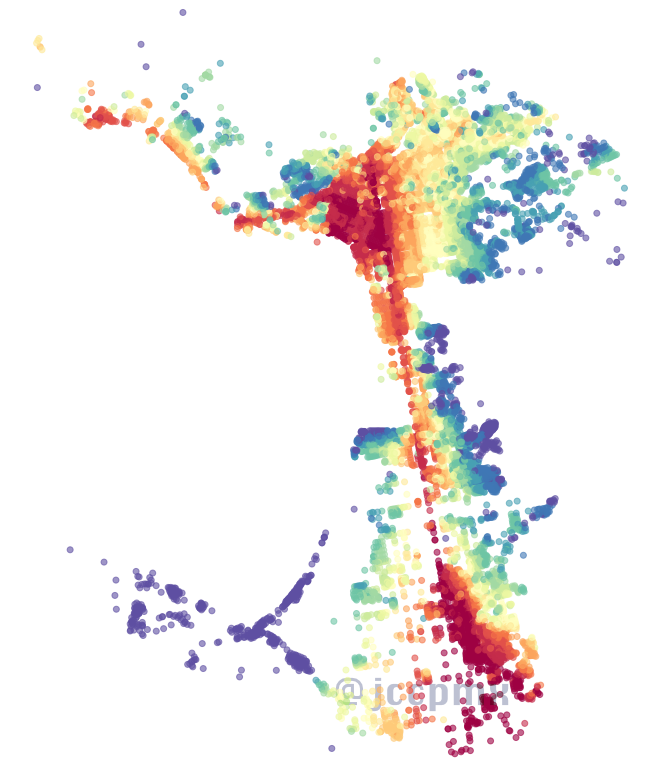
Valor de nodo promedio en calles
En algunos casos, es más fácil comprender los resultados de centralidad si se adjuntan a segmentos de calles, en lugar de intersecciones.
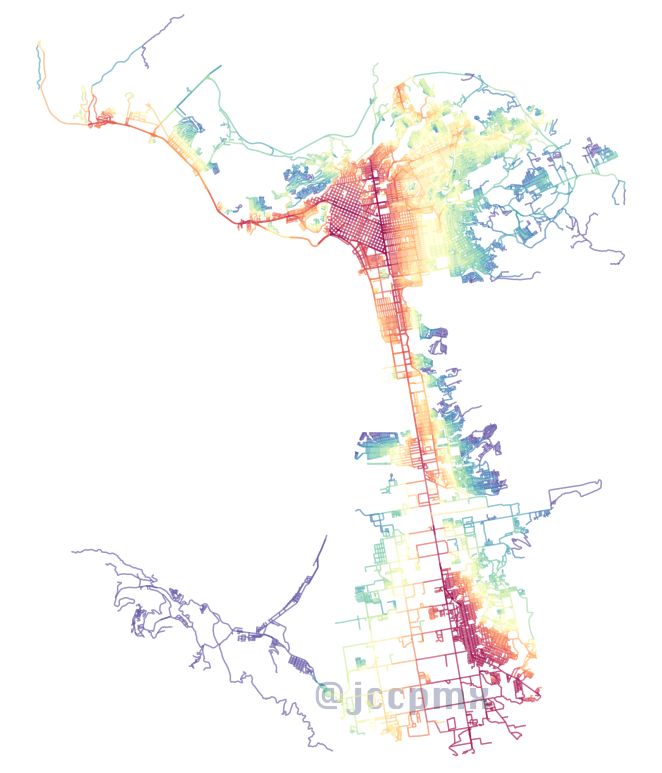
Cercanía por distancia y nodo promedio
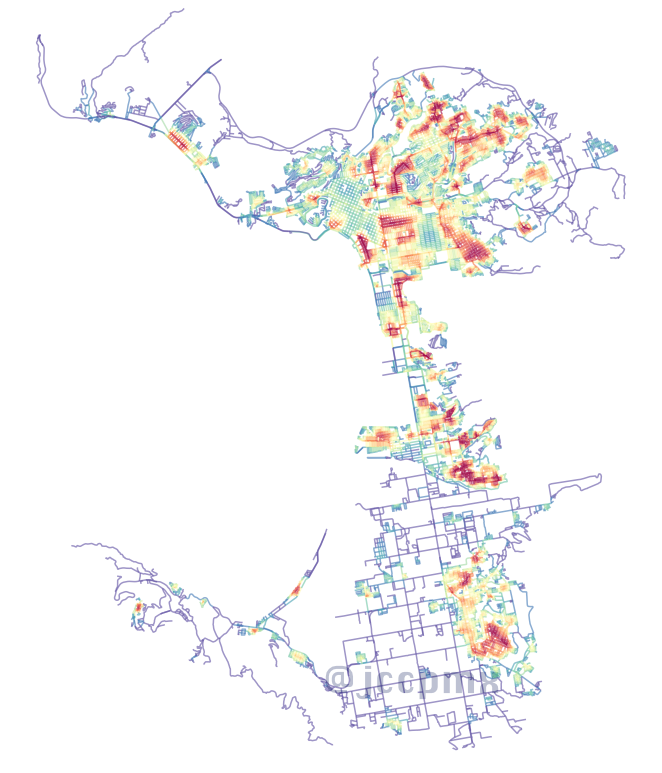
Cercanía media global basada en nodos
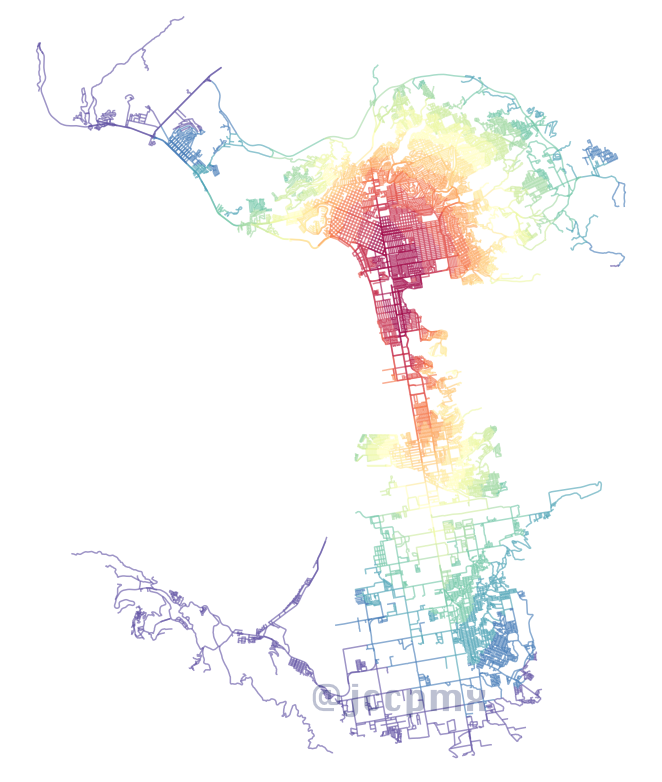
Media por nodo de intermediación
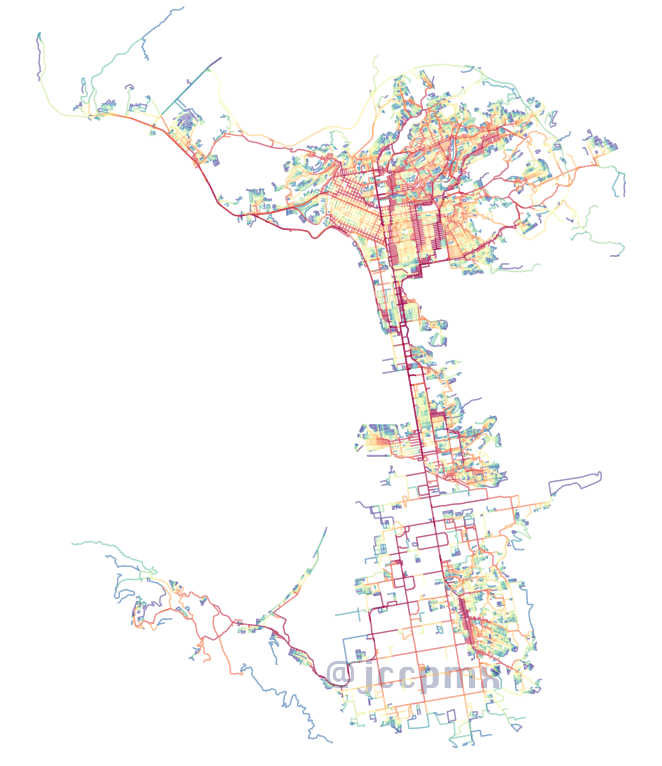
Cercanía angular
Cercanía angular local con una distancia topológica de 5 pasos.
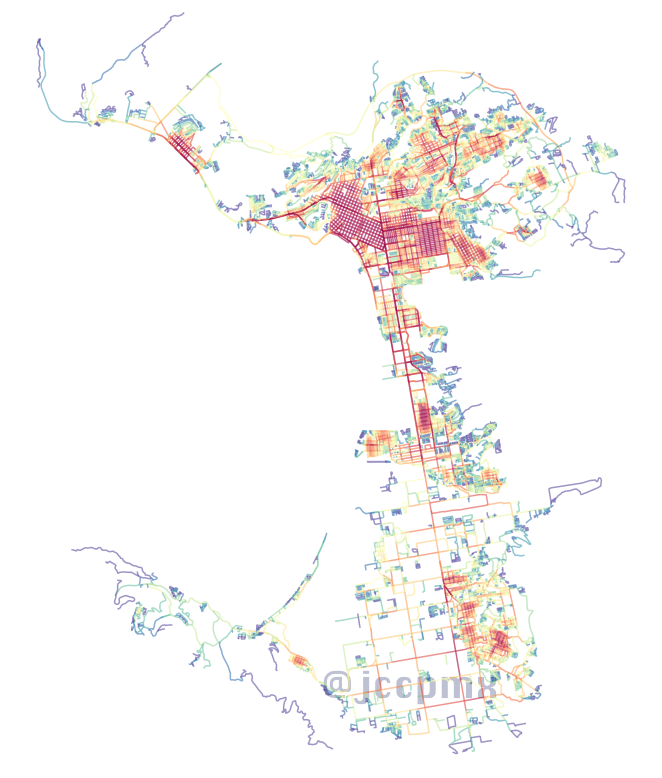
Cercanía angular global
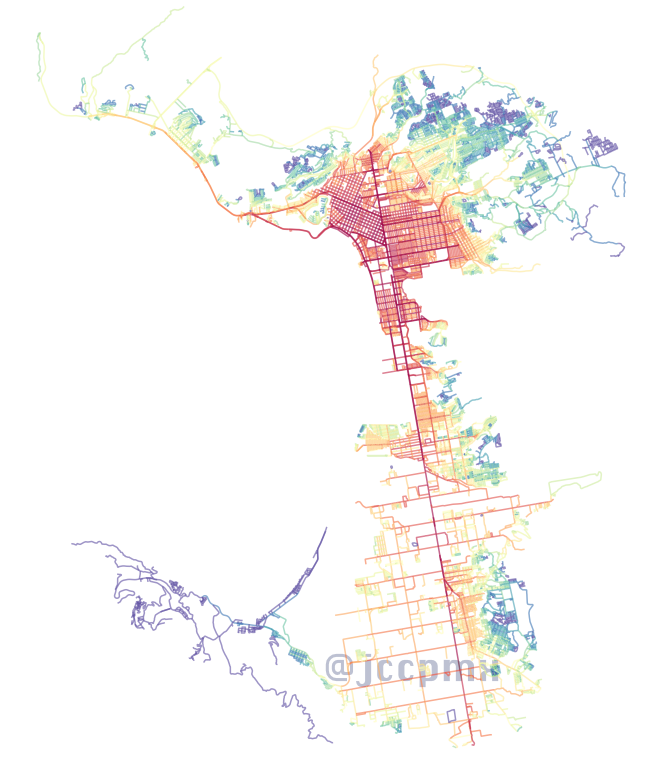
intermediación angular
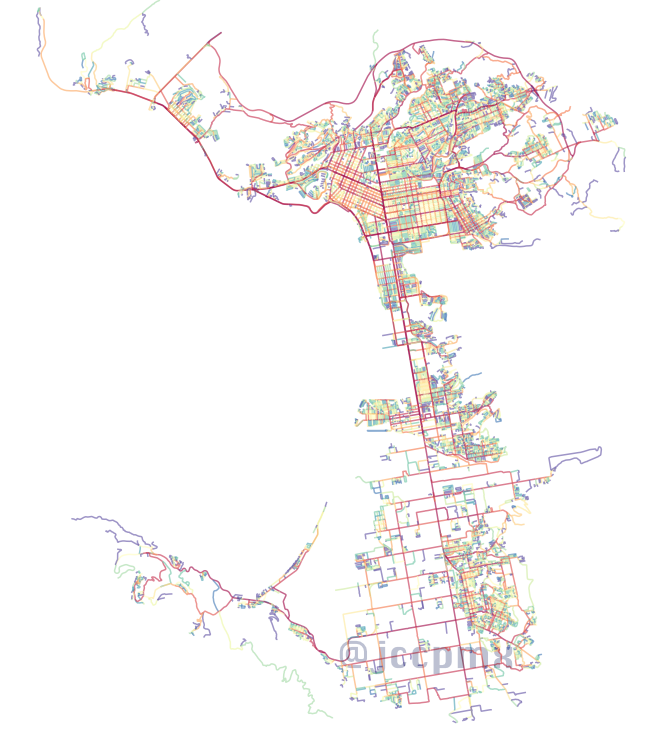
Hasta aquí por ahora, espero que con lo anterior puedan tener una idea global de como se pueden descubrir patrones y estructuras en las calles.
Salut!